4.Prolog言語
本章では、Prolog言語そのものに焦点を当て、プログラムで扱えるデータ構造(4-1)、プログラムの基本構造(4-2)、プログラム実行のメカニズム(4-3)、Prolog言語の構文(4-4)について順に解説します。
4-1.Prologのデータ構造
Prologが扱うデータは、項(term)と呼ばれます。大きく分けると、項には単純項と複合項の2種類があります。
単純項はPrologの基本的なデータ型で、これ以上細かく分解出来ないようなデータを表します。
単純項には定数と変数があります。
複合項は、いわゆる配列のように、複数のデータを一括して扱うためのものです。
つまり、幾つかの項をまとめ上げて一つの複合項は作られます。
逆に、一つの複合項を分解して、その構成要素を取り出す事も出来ます。
複合項は、配列よりはるかに柔軟なデータ構造を扱えます。
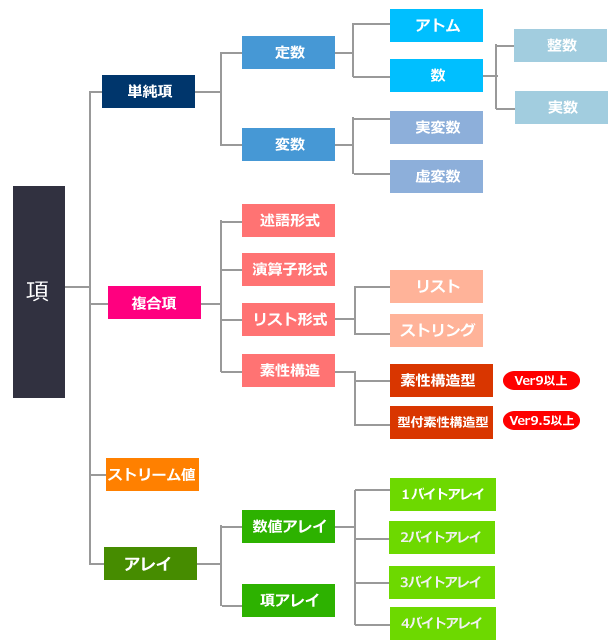
「項」は次のように分類されます。
4-1-1.定数
定数とは、プログラムの実行中に値が変化しないような単純項です。
例えば、次のようなものが定数です。
110 0 -1.2 漢字 penguin 'this-is-a-constant'
定数には、主として次の3つのものがあります。
[1]整数値
整数値の表現には次の3種類があります。
- 10進表現
0から9までの数字の列
- N進表現
最初1文字が基数を表す0から9の数字で、2番目が引用符号「'」で、3番目以降に0から9までの数字の列が続くもの。
ただし、最初の1文字が0のときは、16進数と見なし、aからfまたはAからFの英文字が混じってもよい。
また、最初の1文字が0のときは2番目が引用符号「'」に代え、0xffffのように「x」でもよい。 - 文字キャラクタコードと制御コードの表現
・c'に続く'¥'を除く1文字はその文字コードを表します。
<例>| ?- A = [ c'a, c'A, c'%, c' , c',,c'あ ]. A = [97,65,37,32,44,33440] yes
・c'¥¥ は ¥の文字コードを表します。
<例>| ?- A is c'¥¥ . A = 92 yes
・c'¥ に続く次の1文字は制御コードを表します。これ以外はエラーとなります。
b backspace (character code 8) t horizontal tab (character code 9) n newline (character code 10) v vertical tab (character code 11) f form feed (character code 12) r carriage return (character code 13) e escape (character code 27) d delete (character code 127) a alarm (character code 7)
<例>| ?- X = [ c'¥b ,c'¥t ,c'¥n ,c'¥v ,c'¥f ,c'¥r ,c'¥e ,c'¥d ,c'¥a ]. X = [8,9,10,11,12,14,27,127,7] yes | ?-X is c'¥A. Syntax error
【プログラムコンサルト時、READ時の整数値オーバーフロー】
プログラムに記述された整数値や実行時に読み込まれる整数値は整数の有効範囲でなければなりません。
32ビット版 -2147483648~2147483647 64ビット版 -9223372036854775808~9223372036854775807 これを超える場合はエラーとなりますが、エラーとしたくない場合、組込述語 s_int_ovf_mode/2で抑止できます。
| ?-read(X). |: 0xfffffffffffffffffffffff. Illegal argument supplied ---- Backtrace read(X_12) ?- | ?-s_int_ovf_mode(_,off). _.2 = on yes | ?-read(X). |: 0xfffffffffffffffffffffff. X = -1 yes
[2]実数値
実数は仮数と指数に分けて表現される数です。仮数と指数は「e」か「E」で区切ります。
指数が「1」の場合は「e」か「E」の区切りと指数を省略できます。
[3]アトム
アトムとは、以下の条件の何れかにあてはまる定数を指します。
-
英数字、仮名漢字、及びアンダーラインを組み合わせた文字列で、先頭の文字が英小文字または仮名漢字で始まるものです。
-
引用符号「'」(シングルクウォート)で囲まれた文字列、ただしこの文字列中に「'」自身を入れたい時は「''」のように続けて2回書く必要があります。
-
「+」「-」「*」「/」「¥」「^」「 <」「> 」「=」「`」「:」「.」「?」「@」「#」「$」「&」からなる文字列。ただし、最初の2文字が「/*」でないもの(「/*」は、コメントの始まりを表します)。
-
「;」「!」「[]」「{}」「¦」のうちのどれか。
なお、アトムの長さは65,535文字以下でなければなりません。
4-1-2.変数
変数と見なされる文字列の条件は次の通りです。
英大文字またはアンダーライン「_」一文字か、これらで始まり、英数字、仮名、漢字などの全角文字及びアンダーラインより構成される文字列(これら以外の記号が含まれる事は許されません)。このうちアンダーライン「_」一文字の変数を虚変数と呼びます。この虚変数に代入された値(項)は参照できません。虚変数は同一節に複数出現したとしても異なる変数とみなされます。したがって、虚変数は複合項のアリティを合せる為のダミー変数としても使われます。
変数名の長さは65,535文字以下でなければなりません。また、1つの節の中で使用できる変数の数は65,535個以下となります。
4-1-3.定数と変数の有効範囲
定数(または変数)の有効範囲とは、プログラム中で2つ以上の同じ名前の定数(または変数)が常に同じものを意味する範囲のことです。
話を具体的にするために、下のプログラムに注目してください。
| 理解する(松尾さん,ワビ).↓ /*松尾さんは“ワビ”がわかる。*/ | 理解する(松尾さん,サビ).↓ /*松尾さんは“サビ”がわかる。*/ | 理解する(ブリキ屋さん,サビ).↓ /*ブリキ屋さんは“サビ”がわかる。*/ | 理解する(X,風流):- 理解する(X,ワビ).↓ /*“ワビ”がわかる人は風流を理解する。*/ | 理解する(X,風流):- 理解する(X,サビ). /*“サビ”がわかる人は風流を理解する。*/
この中には「松尾さん」というアトムが2ケ所に出現します。
すなわち「理解する(松尾さん,ワビ).」の中と「理解する(松尾さん,サビ).」の中です。
この2つの「松尾さん」は同一人物「松尾さん」を意味します。
別の言い方をすれば、この2つの「松尾さん」は全く同じものを表わしています。
もし、最初の「松尾さん」を別のアトム「芭蕉さん」で置き換えればこのプログラムは全く異なる挙動を示すでしょう。
一方、このプログラム中に変数Xは4ケ所出現します。
すなわち、
| 理解する(X,風流):- 理解する(X,ワビ).
の中に2ケ所と,
| 理解する(X,風流):- 理解する(X,サビ).
の中に2ケ所です。
ところが、この4つのXはすべて同じものを意味する必要はありません。
最初の節の2つのXは同じもの(例えば「松尾さん」)を意味しなければいけませんし、2番目の節の2つのXも同じもの(例えば「ブリキ屋さん」)を意味しなければいけません。
しかし、最初の節のXと2番目の節のXは別のもの(例えば前者が「松尾さん」で後者が「ブリキ屋さん」)を意味しても一向にかまわないのです。
実際、
| 理解する(X,風流):- 理解する(X,ワビ).
の中のXを、別の変数「Y」で置き換えて、
| 理解する(Y,風流):- 理解する(Y,ワビ).
としても、プログラムは同じように動くはずです。
つまり、同じ名前の定数はプログラム全体で同じで、ある決まったものを意味しますが、同じ名前の変数は1つの節の中でだけ同じで、まだ決まっていない何かを意味するのです。
したがって、定数の有効範囲はプログラム全体に及びますが、変数の有効範囲は1つの節の中にしか及びません。
余談ですが、上のプログラムで最初の「サビ」は抽象的概念としての「寂」を意味し2番目の「サビ」は金属が酸化してできた「錆」を意味すると考えるのが自然でしょう。すると、このプログラムは定数の有効範囲を誤って作られたことになります。
(勿論、「寂」を理解するブリキ屋さんもいらっしゃるでしょうが・・・)
4-1-4.複合項
複合項は本質的に述語形式で表現できます。したがって、述語形式以外の複合項でも、すべて述語形式で表現することが出来ます。
複合項の一般論として、複合項は他言語における関数とは異なり、複合項自身は値を持っている訳ではありません。
例えば「a(1,2) = 7.」として「a(1,2)」自身に「7」を代入するものではありません。
「a(1,2)」は単に「a」という名前の値が二つ入る入物に「1」と「2」が入ったものと考えてください。
複合項には、以下の3つの形式があります。
- 述語形式(ファンクタ、述語)
- 演算子形式
- リスト形式(リスト、ストリング)
Ⅰ.複合項・述語形式(ファンクタ、述語)
述語形式の複合項は、一般的な手続型言語における関数呼び出し形式と同様の記法を用いて書き表されます。
| <形式> | 述語名 | (引数1,引数2,引数3,・・・・引数n) |
| ┃ | ┗━ 引数の数nをアリティという(0 < n ≦ 65,535 とする) | |
| 述語名はアトム | ||
<例>pair(リンゴ,apple)
f(2,3,5)
zoo(パンダ,ペンギン,カバ)
'A'((b(1),v(2)))
データ(A,M)
名前(山田)
※述語名を「ファンクタ」または単に「述語」とも呼び、引数を「アーギュメント(argument)」と呼ぶ場合もあります。
また、述語の引数の個数をアリティと呼びます。
Ⅱ.複合項・演算子形式
演算子形式の複合項は、アリティ(述語の引数の個数)が1または2の述語形式の複合項をオペレータ宣言して、数式のような記法を可能にしたものです。
<形式>「引数1 演算子 引数2」 「演算子 引数」 「引数 演算子」
例えば、「X is 1 + 2」も実は「is(X,+(1,2))」という述語形式の複合項と等価なのです。
つまり演算子は述語名にあたります。よって演算子は全てアトムです。アリティが1の場合も同じです。「spy p」は「spy(p)」と等価です。また、節の中のゴールの区切りである「,」や「;」も演算子の一種です。
オペレータ宣言の詳細については「4-3-5.オペレータ」を参照してください。
Ⅲ-(1).複合項・リスト形式 - リスト
リスト形式の複合項は、要素となる項の並びをカギカッコ(「[」と「]」)で囲ったもので、要素の数は可変長で、多くの手続型言語における配列のように予め要素の数を宣言する必要がなく、リストを繋いで要素を追加したり、分割して取り除いたりという操作が自由に出来ます。
<形式> [要素1,要素2,要素3,・・・要素n]
リストの要素は通常「,」(カンマ)で区切られますが、区切り記号「|」(バーチカルライン、縦棒)で区切った場合は特別の意味を持ちます。リスト同士をユニファイする場合には、「|」の前までは対応する位置の要素同士がユニファイされますが、「|」の後の部分は残りの要素のリストがユニファイされます。
<例>
| ?-[X,Y|Z]=[a,b,c,d,e].
X = a,
Y = b,
Z = [c,d,e]
リストも実は述語名がピリオド「.」、アリティが2の述語なのです。
つまり、 [a,b,c,d] は .(a,.(b,.(c,.(d,[])))) と等価です。
最後の「[]」は空リストと呼ばれ、リストの最後の要素は通常は空リストになっていますが、カギカッコで括った表現では最後の空リストは見えません。
ただし、[a,b,・・・|x]と書いた場合に限り「x」がリストの最後の要素となり、この場合は空リストは見えないのではなく存在しません。
Ⅲ-(2).複合項・リスト形式 - ストリング
ストリングとは、「"」(ダブルクォート)以外の任意の文字を「"」で囲んだもの、または「""」のみからなる文字列(長さ0でもよい)です。
<形式>"任意の文字の並び"
「"」自身を文字列に入れる場合は「""」とします。
例えば 「コレハ"カバ"デス」という文字列をストリングとして扱うためには「"コレハ""カバ""デス"」と書かなければいけません。
<例>"Panda" "漢字" "200" "I Know Prolog."
また、ストリングの実体は文字コードのリストです。
例えば、"Panda" は [80,97,110,100,97] と等価です。
漢字などのマルチバイト文字の場合も、通常使用されるエンコードに応じた漢字コードのリストになります。
例えば、"漢字" は、Shift_JISコード(2バイト文字)では [35519,36506] となり、UTF-8コードでは [15121570,15052183]となります。
ただし、漢字モードが「off」の場合は、1バイトずつに分けて扱われます。従って、"漢字" はShift_JISなら [138,191,142,154] 、UTF-8なら [230,188,162,229,173,151] となります。
<形式2>"任意の文字の並び"変数
ストリングに続き変数を記述すると文字コードリストの尾部変数となります。
<例>
| ?- X="Panda"L. X = [80,97,110,100,97|L_13], L = L_13 yes
Ⅲ-(3).複合項・素性構造型
素性構造型とは、
<素性と値の対>
の集合です。AZ-Prologでは、ICOTで開発されたProlog処理系、CU-Prolog,CILのシンタックスを採用し、中括弧に挟まれた任意の個数の
<素性と値の対>
をカンマで並べた表記をとります。
空を除き
<素性と値の対>
を一つも要素としない場合は従来構造として扱いますのでDCGの補強項も問題なく記述できます。
<素性と値の対>
とそれ以外の項との混在はエラーです。
また、素性は同一階層においてはユニークで、アトムでなければなりません。
<素性と値の対>
はアトムである素性と区切り記号(デフォルトでは":" 変更可)で接続した素性構造型を含む任意の項で表します。
デフォルトでは素性構造を取り扱いますが、上記に抵触するようなプログラムの場合は、素性構造を取り扱わないモードへの切り替えも用意されています。
<素性構造の例>
{} %% 空の素性構造
{ 氏名:山田太郎,生年月日:{年:1951,月:5,日:26},趣味:X }
・この素性構造は属性値行列(attribute value matrix、AVM)で次のように表記されます。
|~ 氏名 山田太郎 ~|
| |
| |~ 年 1951 ~| |
| 生年月日 | 月 5 | |
| |_ 日 26 _| |
| |
|_ 趣味 X _|
<素性構造でない従来型中括弧構造の例>
{write(X),nl}
<エラーとなる例>
{ category:noun_phrase, category:verb_phrase } 同じ階層に同一素性が含まれている
{ category:noun_phrase,A } <素性と値の対>と<素性と値の対>でない項とが混在している
{ category:noun_phrase,Z:single } 素性がアトムでない項が含まれている
素性構造の単一化など詳細は、本マニュアル 9-2.素性構造型(Feature Structure型)に書かれていますのでご参照ください。 4-1-5.ストリーム値
「ストリーム値」とは一般のファイル名の事ではなく、入出力ファイルを識別するための内部値です。
<表示形式>fp_XXXXXX
下の例からも分かるように、ストリーム値はこのような形式をしていますが、いわゆるファイルポインタと同様に考えればよく、自分で値を決める性質のものではありません。
ストリーム値は「see/2」「tell/2」「tella/2」によって入出力オープンした場合にこれらの述語の第2引数にユニファイされます(返される)。以降、ストリーム指定の出来る入出力述語(「read/2」「write/2」「writeq/2」「get0/2」「get0/2」「put/2」「listing/2」)を使う場合にファイル名の代わりにこのストリーム値で指定します。
なお、この値はアトムでないため、アトムレジスタへの保存することはできません。また、この値に分解・結合などの操作を加えることは許されず、意味がありません。
<例>‘abcde’というアトムを‘abc.txt’というファイルに書き込む。
¦?-tell('abc.txt',S),write(S,abcde),told(S).
S = fp_885f40
yes
4-1-6.アレイ
AZ-Prologで扱えるアレイは、任意の項を格納できる「項アレイ」、および、指定したバイト数の整数値を格納する「整数アレイ」のいずれかの配列型です。アレイのサイズは生成時に指定し、固定です。
アレイのインデクス(要素の位置を示す整数)は0から始まります。
大域的な領域が確保され、アレイのインデクスを指定してデータを設定、取得することができます。
「assert」「retract」と同様、述語呼び出しの副作用として値が設定変更されるので、バックトラックによって取り消されることはありません。
参考:
| create_array/2 | 項アレイの生成 |
| create_array/3 | 整数アレイの生成 |
| set_array/3 | アレイに値を設定 |
| get_array/3 | アレイから値を取得 |
| array_register/3 | arrayレジスタの値を取得・変更 |
<例>
| ?-create_array(100,Array),set_array(Array,0,a(1)),get_array(Array,0,V). Array = array_57081856 V = a(1) yes
4-2.プログラム
Prologのプログラムは下記の (1) または (2) の形をしたものからなります。
これらを節(「ホーン節」と呼ばれることもあります)と呼びます。
プログラムには、このように「規則」と「事実」と呼ばれる形式があり、「規則」は「頭部」と「本体」に別れます。
(1) |
<項> |
:- |
<項>(ゴール)の並び<終止符> |
・・・ |
規則 |
|
頭部 |
|
本体(ゴール列) |
(2) |
<項> | <終始符> |
・・・ |
事実 |
|
頭部 |
|
ただし、ここで各 <項> はアトムまたは複合項です(これらの一部が変数であってもその値がアトムまたは複合項ならば許されます)。
<終止符>はピリオド「.」とキャラクタコードが32以下の文字の二文字からなる文字列です。通常はピリオド「.」とキャリッジリターンとの組合わせで使い、ソースファイルは一行に複数の節を書く事はしませんが、文法上は例えばキャリッジリターンの代りにスペースでもよいので、一行に複数の節を書く事も許されます。
(1)の<項>と(2)の最初の<項>をこれらの節の頭部と呼びます。
また、(1)の二番目以降の<項>の列をこの節の「本体」または「ゴール列」と呼びます。そして、ゴール列中の各<項>を「ゴール」と呼びます。
(2)の形の節は「事実」と呼ばれる節で(1)の形の節の本体がない特別のものと考えることもできます。
次のものは(2)の形の節です。
| 理解する(松尾さん,ワビ).↓
| 理解する(松尾さん,サビ).
これらの場合、「理解する」を「述語名」(または「述語」)と呼びます。より正確には、<頭部>または<ゴール>がアトムである時はそのアトム自身を、複合項の時はそのファンクタを述語名(または述語)といいます。
「松尾さんはワビを理解する。」という日本語の文章を考えた場合、「理解する」の部分が述語(または述語名)と呼ばれますから、この命名は自然なものであるといえます。
また、同じ述語名とアリティの頭部を持つ節の集りをこれまた述語と呼ぶ事もあります。
ここでは単に「述語」と呼んだ場合、特に断わりが無い限りは「同じ述語名とアリティの頭部を持つ節の集り」を指すものとします。
また、次のものは(1)の形の節です。
| 理解する(X,風流):- 理解する(X,ワビ).↓
| 理解する(X,風流):- 理解する(X,サビ).
最初の節の頭部は「理解する(X,風流)」で、その述語名は 「理解する」 です。また、このゴールは「理解する(X,ワビ)」で、その述語名はやはり「理解する」です。
この節は「Xがワビを理解するならば、Xは風流を理解する」または「Xが風流を理解するためには、Xがワビを理解すればよい」と読みます。
このように、規則は「条件付の事実」と考える事ができ、ゴールはその条件に相当します。
つまり「Xがワビを理解する」という事象が真である(つまり条件が満たされる)時、「Xは風流を理解する」という事象が真(つまり「事実」)となることを表します。
Prologのプログラムはそれ自身が事象を表しています。
ゴールは「~ならば」という条件を表し、頭部は「~は~である」という事実を表します。
従って、ゴールのある(条件付の)節は条件が満たされるならば正しいという「規則」(ルール)であり、逆にゴールの無い頭部だけの節は文字通り無条件に正しい「事実」と言える訳です。
そして、ついでに言えばプログラムの実行はその事象が「真」か「偽」か(正しいかどうか)を調べる事なのです。
一般に、節が次の形をしているとすると、
<頭部>:-<ゴール1>,<ゴール2>,……,<ゴールn>.
これは、
<ゴール1>,<ゴール2>,……,<ゴールn>
がすべて正しければ<頭部>は正しい、または<頭部>の条件を満たすためには、
<ゴール1>,<ゴール2>,……,<ゴールn>
の条件がすべて満たされればよいと読む事が出来ます。
したがって、もし次のような節があれば、
| 理解する(X,風流):-理解する(X,ワビ),理解する(X,サビ).
これは「Xがワビを理解し、かつサビも理解するなら、Xは風流を理解する」という意味になります。
一方、もし次のような節があれば、
| 理解する(X,風流):-理解する(X,ワビ);理解する(X,サビ).
これは、「Xがワビを理解するか、あるいはサビを理解するなら、Xは風流を理解する」という意味です。つまり、ゴールを 「,」で区切ると「~かつ~(英語のand)」という意味が生じ、「;」で区切ると「~または~(英語のor)」の意味が生じる訳です。
また、「;」を使うかわりに、
| 理解する(X,風流):- 理解する(X,ワビ).↓ | 理解する(X,風流):- 理解する(X,サビ).
と2つの節を並べて書く事もできます。どちらの書き方をしても実行結果は、ほぼ変りません。
「;」を用いた方が簡潔に書けますが、「;」を多用するとプログラムが見にくくなり実行過程が把握しにくくなりますし、どちらかというと二つの節に分けて並べて書いた方が「Prologらしい書き方」と言えるかも知れません。
プログラムが書けたら、これを実行しなければ意味がありません。
プログラムを起動するためには、次の(3)または(4)の形のゴール列を入力してやればよいのです。
(3) :-<ゴール>,<ゴール>,……,<ゴール><終止符>
(4) ?-<ゴール>,<ゴール>,……,<ゴール><終止符>
(3)の形のゴールの並びを「コマンド」,(4)の形のゴールの並びを「質問」と呼びます(この違いは「質問」はその真偽を「yes」「no」で画面に表示するのに対し、「コマンド」はそれらを表示しない点だけです)。
どちらの場合にも、プログラムが実行される事(すべての<ゴール>が正しいかどうか調べられる事)には変りありません。
プログラムの実行については「4-3.プログラムの実行」を参照してください。
<補足>
自然言語の文法規則を表現するDCG形式の記述も可能(その良い例としては、CGIのサンプルプログラムに「積み木の世界」があります。sample/cgi_demo/cgi-bin/tumiki.dcgを参照してください)ですが、コンサルト時に前述の規則/事実いずれかの節の形に変換されます。これについては「5-3-2.ファイルからのプログラム入カ」の最後にある
<補足1>
も参照してください。DCGの詳細については他書に譲ります。
4-3.プログラムの実行
「4-2.プログラム」で説明した通り、Prologのプログラムの実行は節によって表現された事象が正しいかどうか(真か偽か)を調べる(証明する)事が主目的です。
手続型言語に於ける手続き(例えば、画面に文字を表示する、数式の解を求めるなど)はPrologでは事象の証明過程の副作用と見なします。
勿論、実際にはその副作用が主目的である事の方が多いのですが、Prologプログラムを実行する側(つまり処理系側)から見れば証明が主目的で、手続きはその過程の一部として、しかたなく行なわれる作業です。
例えば
write('あいうえお')
というゴールがあったとすると、処理系はそのゴールの証明に取り掛かります。
「write/1」という頭部を持つ節は標準組込述語(処理系が予め内部的に持っている述語)として登録されているためそれを実行することになります。
組込述語の多くは所定の副作用を持っていて、処理系が証明過程(プログラムの実行過程)でそのゴールを調べようとすると、その副作用が実行されるようになっています。
「write/1」の場合はその述語名の通り、引数の項を出力する副作用を持っていて、その副作用(項の出力)を完了すれば「真」になります。
また組込述語の場合は、その個々の副作用の性格により証明(実行)結果として「真」「偽」の他に「エラー」が加わる述語もあります。
通常は実行時エラーが発生するとその時点で実行が中断されます。
このようにPrologプログラムの実行過程はすべて「証明過程」であると言えます。
ここにPrologが「論理型言語」と呼ばれる所以(ゆえん)があります。
4-3-1.単一化(ユニフィケーション、ユニファイ)
ある2つの項に対し、それらが等しいかどうかを調べたり、それらの中に未代入の変数が出現する場合には、その変数に適当な項を代入してその2つの項が等しくなるようにしたりすることをユニフィケーション、またはユニファイ、または単一化と呼びます。
ユニファイには次の4つの場合の規則が考えられます。
- 二つの項がどちらも定数(または定数が代入された変数)の場合、双方の定数が等しければユニファイが成功し、等しくなければ失敗します。
- 二つの項のうち、どちらか一方が定数(または定数が代入された変数)で、他方が未代入の変数の場合、未代入の変数に定数が代入されて、ユニファイは必ず成功します。
- 二つの項がどちらも未代入の変数の場合、ユニファイが必ず成功し、その節内に於いてこれらの変数は同じ変数として扱われます。つまり、どちらかの変数に定数が代入されると他方の変数にも同じ値が代入されます。
- 複合項同士の場合、まずファンクタとアリティを調べ、もし違えばユニファイは即失敗します。それらが同じであった場合はその引数のユニファイに掛ります。
複合項の引数のユニファイは、並び順で対応する個々の引数同志について上記規則を再度適用することになります。そして、全ての引数のユニファイが成功に終った場合にのみ複合項のユニファイが成功し、それ以外は失敗します。
例えば
理解する(ブリキ屋さん,サビ)
という複合項と
理解する(X,サビ)
という複合項のユニファイをしたならば、先ず「理解する」が同じである事が確認(ユニファイ)されます。
次にどちらの複合項もアリティが2である事が確認されます。
それらが確認されたら、引数の値(「ブリキ屋さん,サビ」と「X,サビ」)のユニファイに取り掛かります。
先ず、第一引数の「ブリキ屋さん」と「X」のユニファイを試みます。
「X」が未代入の変数であるとすると、上の「2.」の規則にしたがって「X」に「ブリキ屋さん」が代入されて「ブリキ屋さん」と「X」のユニファイは成功します。
次に第二引数が「サビ」と「サビ」なのでユニファイは問題無く成功します。
この結果、「ファンクタ」「アリティ」「引数の内容」ともにユニファイが成功したので、「理解する(ブリキ屋さん,サビ)」と「理解する(X,サビ)」とのユニファイは成功し、「ブリキ屋さん」が「X」に代入されます。
理解する(ブリキ屋さん,サビ) | | | 理解する( X , サビ)
また「理解する(松尾さん,X)」と「理解する(Y,サビ)」とをユニファイすると、その結果、「X」に「サビ」を、「Y」に「松尾さん」を代入してユニファイは成功します。
4-3-2.Prologの実行
Prologプログラムはどうやって実行されるのかを考えてみましょう。
Prologプログラムの実行は一言で云うと「ある事象が正しいかどうか(事実かどうか)を調べる(判断・判定する)過程」となります。
また、Prologプログラムは「~は事実か?」という質問で起動されます。
プログラムの具体的な例として次のプログラムを考えてみます。
[1] | 理解する(松尾さん,ワビ).↓
[2] | 理解する(松尾さん,サビ).↓
[3] | 理解する(ブリキ屋さん,サビ).↓
[4] | 理解する(X,風流):- 理解する(X,ワビ).↓
[5] | 理解する(X,風流):- 理解する(X,サビ).
まず、次の質問(頭部の無い本体{ゴール列}のみの節)を入力した場合を考えてみましょう。
[6] | ?-理解する(松尾さん,風流).
この時Prolog処理系は、[6]のゴールが正しいかどうか判定に行きます。
一般にあるゴールが正しいかどうか判定することを、ゴールの実行と呼びます。
[6]のゴールを実行するために、Prolog処理系は「理解する(松尾さん,風流)」とユニファイできる頭部を持った節を上から順番に探索します。
今の場合、まず[4] の節が探しだされるでしょう。
[6]のゴールとユニファイすることにより、[4]は次の[4']になります。
[4'] 理解する(松尾さん,風流):-理解する(松尾さん,ワビ).
[6]の質問の意味は「松尾さんは風流を理解するか?」です。そして、[4']の節の意味は「松尾さんが風流を理解するためには、松尾さんはワビを理解すればよい。」です。したがって、[6]の質問に答えるためには、松尾さんがワビを理解するかどうかがわかればよいことになります。
そこでProlog処理系は次に[4']のゴール(すなわち「理解する(松尾さん,ワビ)」)の実行を行います。
(規則1)
一般に、あるゴール「G」を実行する時には「G」とユニファイ可能な頭部を持つ節「C」が探しだされ、「C」のゴール列が実行されます。ただし、ユニファイの際に「C」の頭部のある変数に項「T」が代入されたなら、「C」のゴール列に出現する同じ名前の変数にも、同じ項「T」が代入されなければいけません。
さて、[4']のゴールの実行を行うために、Prolog処理系は「理解する(松尾さん,ワビ)」とユニファイ可能な頭部を持つ節を上から順番に探索します。
そして[1]の節がみつけだされます。[4']のゴールの実行の目的は「松尾さんはワビを理解する。」かどうか判定することにありました。
一方[1]の節は「松尾さんはワビを理解する。」という意味ですから[4']のゴールは正しいことがわかります。
したがって[4']のゴールの実行は成功し、その結果[6]の質問も正しいことがわかります。
(規則2)
一般に、あるゴール「G」を実行するときに「G」とユニファイ可能な頭部を持つ節「C」が探しだされ、しかも「C」がゴール列を持たなければ、「G」の実行は成功します。
では次に、変数を含む次の質問がどのように実行されるか考えてみましょう。
[7] | ?-理解する(松尾さん,X).
この場合もまず、[7]のゴールとユニファイ可能な頭部を持った節が上から順番に探しだされます。
最初に[1]が探しだされるでしょう。
このユニファイによって、[7]の「X」には「ワビ」が代入されます。
[1]はゴール列を持ちませんから、規則2により[7]のゴールは成功します。
そしてユニファイによって得られた情報から、「X」が「ワビ」であれば「松尾さんは“X”を理解する」が正しいことがわかります。
すなわち、質問のゴール列中に変数が出現する時、この変数にどんな項が代入されればゴールが正しくなるかはユニファイの過程で知ることができるのです。
尚、[7]の質問の場合、松尾さんが理解するものとして「ワビ」以外の答えが要求されたら、処理系は[7]のゴールとユニファイ可能な頭部を持つ別の節を探しに行きます。この場合、まず[2]の節が探しだされ、「松尾さんがサビを理解する。」ことがわかります。
4-3-3.バックトラック
Prologの実行の解説で使われた次のプログラムで、[8]のゴールはどのように実行されるか考えてみましょう。
[1] | 理解する(松尾さん,ワビ).↓ [2] | 理解する(松尾さん,サビ).↓ [3] | 理解する(ブリキ屋さん,サビ).↓ [4] | 理解する(X,風流):- 理解する(X,ワビ).↓ [5] | 理解する(X,風流):- 理解する(X,サビ).↓ | ↓ [8] | ?-理解する(ブリキ屋さん,風流).
この場合もまず「理解する(ブリキ屋さん,風流)」とユニファイ可能な頭部を持つ節が探され[4]が最初に選びだされます。
このユニファイによって、[4]の「X」には「ブリキ屋さん」が代入されます。
したがって、次に実行すべきゴールは「理解する(ブリキ屋さん,ワビ)」になります。
ところが、これとユニファイ可能な頭部を持つ節は[1]~[5]の中に存在しませんから、このゴールは失敗します。
あるゴールの実行が失敗すると、処理系はバックトラック(後戻り)と呼ばれる作業をします。
この場合[8]のゴールとユニファイ可能な頭部を持つ[4]以外の節が探しに行かれます。
すると、今度は[5]の節がみつかり、さらに実行が続けられるのです。
[8]のゴールは、もともと[4]及び[5]の頭部とユニファイ可能でした。
しかし[4]のゴールと[5]のゴールを同時に実行することはできません。
そこで、まず[4]のゴールを実行してみて、失敗したら[5]のゴールを実行してみるというのがバックトラックなのです(ちょうどある人が道を歩いていると三叉路に出くわしてしまい、どちらに行ったらいいのかわからないので、まず左の方へ行ってみて、もし行き止まりならその三叉路まで戻って右の方へ行きなおすという状況に似ています)。
尚、バックトラックが行われる時には、失敗したゴールを実行する際に行われたユニファイはすべてキャンセルされます。例えば[8]のかわりにつぎの[8']のゴールが実行され、これが[4]の頭部とユニファイされたとします。
[8'] | ?-理解する(ブリキ屋さん,Y).
すると、このユニファイによって「Y」には「風流」が代入され[8']のゴールは
理解する(ブリキ屋さん,風流)
となります。そして[4]のゴールはやはり失敗します。
ここでバックトラックが行われると、このユニファイの影響が帳消しにされて、再び[8']のゴールは「理解する(ブリキ屋さん,Y)」に戻りこのゴールの実行が続けられるのです。
このバックトラックとユニファイの機能のおかげで、通常の言語では解きにくい問題でも、Prologを使うと簡単に解ける場合がよくあるのです。
4-3-4.カット
バックトラックによって、Prolog処理系はゴールに他の解が無くなるまで試行錯誤をくり返します。
ところがこの試行錯誤は網羅的に行われますから、初めから失敗するとわかっているゴールを実行するために多くの時間をさく場合があります。
そういう場合、特別の述語「!」(カットと読みます。)を用いることによってバックトラックの制御を行うことができます。
例えば、次のプログラムを見てください。
これらは「ある遊園地に入場するために、子供は 500円,大人は 1,000円払う」という意味を持ちます。
[1] | 入場する(X,遊園地):-子供である(X),払う(X,ごひゃくえん). [2] | 入場する(X,遊園地):-大人である(X),払う(X,せんえん).
つまり [1]の節は「“X”が遊園地に入場するためには“X”が子供であり、かつ“X”が 500円払えばよい」という意味ですし、[2]の節は「“X”が遊園地に入場するためには、“X”が大人であってかつ“X”が 1,000円払えばよい」という意味です。
さらに次のようなプログラムが続くとしましょう。
[3] | 子供である(タツヤ君). [4] | 払う(タツヤ君,ひゃくえん).
[3]、[4]はそれぞれ「タツヤ君は子供です」及び「タツヤ君は100円払います」という意味を持ちます。そして、次のような質問を入力してみましょう。これは、「タツヤ君は遊園地に入場できるか?」という意味を持ちます。
[5] | ?-入場する(タツヤ君,遊園地).
この時、処理系はまず「入場する(タツヤ君,遊園地)」と単一化可能な頭部を持つ節を上から順に探し、[1] を見つけます。
単一化によって、[1] の「X」には「タツヤ君」が代入されますから、次には
子供である(タツヤ君),払う(タツヤ君,ごひゃくえん)
というゴール列が実行されます。
このうち「子供である(タツヤ君)」は[3]によりに成功しますが「払う(タツヤ君,ごひゃくえん)」は成功しません。
したがって、バックトラックが起きて、処理系は[5]のゴールと単一化可能な頭部を持つ別の節を探しに行き[2]を見つけだします。
しかし、よく考えるてみるとタツヤ君は子供ですから[2]のゴールは成功するはずがありません。
つまり[1]の最初のゴール「子供である(タツヤ君)」が成功した段階で[2]の節を調べる価値はなくなっていたのです。
このことを処理系に教えてやるためには、[1]のプログラムを[1']のように書き直すといいでしょう。
[1'] | 入場する(X,遊園地):-子供である(X),!,払う(X,ごひゃくえん).
[1] との違いは、「子供である(X)」というゴールの次に 「!」が置かれたことにあります。
では、[1] を[1']で置き換えて、[5]の質問が行われると、処理系はこれをどのように実行するのでしょうか?
まず先程と同様に [1']の頭部と[5]のゴールを単一化して、
子供である(タツヤ君),!,払う(タツヤ君,ごひゃくえん)
が実行されます。
次に「子供である(タツヤ君)」が成功するのも先程と全く同じです。
次のゴール「!」は、ただちに成功する述語です。
ただし、「!」が一旦成功すると、バックトラックによって 「!」が実行される以前の状態に戻る時には、[1']の頭部と単一化されたゴール(すなわち[5]のゴール)を強制的に失敗させます。
したがって、この時[5]のゴールと単一化可能な別の節があっても無視されます。
一般的に言うと、次のようになります。
(a)カットは実行されると直ちに成功します。
(b)カットが実行された以前の状態にバックトラックする時にはこのカットを含む節の頭部と単一化されていたゴールが、強制的に失敗させられます。
4-3-5.オペレータ
(A)オペレータの結合優先順位
ただ、「+(1,2)」を「1+2」と書けるようにしただけでは次の様な問題が出てきます。
それは例えば、「1+2*3」というふうに複数のオペレータを書いた場合に処理系が「(1+2)*3」と解釈したらいいか、「1+(2*3)」と解釈したらいいのか分らなくなってしまう事です。
算数のルールからは「1+ (2*3)」と解釈されなければなりません。
「1+ (2*3)」と解釈させるためには「+」より「*」の方が結合が優先される事を表さなければなりません。そこで考えられたのが「オペレータの結合優先順位」です。
オペレータの結合優先順位は、宣言する際に「1」から「1200」までの整数値で指定します。
この数が小さいほど結合優先順位が高く、逆に大きいほど結合優先順位が低くなります。
なお、オペレータの結合優先順位に関係なく「( )」で囲むとその中が優先されます。
また、「( )」が複数組ある場合はより内側が優先されます。
この、結びつきをどう解釈するかという問題は各オペレータの結合優先順位に差を付けてもまだ解決出来ない事があります。
それは、「同じ結合優先順位のオペレータが並んだ時にどう解釈するか」という問題が残っているからです。
そこでまた考えられたのが「オペレータの型」です。
「オペレータの型」はつまり、「左側の結びつきか、右側の結びつきかどちらを優先するか」という事を決定するものです。
つまり「1+2+3」を「(1+2) + 3」と解釈するのか「1+ (2+3)」と解釈するのかを判断する為のものです。
間置記法のオペレータの型には「xfy」「yfx」「xfx」があります。
ここで、「f」がファンクタをあらわし、「x」と「y」がそのアーギュメントを表わしていると考えるとよいでしょう。「x」と「y」の違いは次の点です。
- アーギュメント「x」が表すアーギュメントの中で1番高い結合優先順位を持つオペレータ(カッコの中に出現するものは除く)が「f」で表されるオペレータの結合優先順位より低い。
- 「y」が表す中で1番大きい結合優先順位を持つオペレータが、「f」で表されるオペレータの結合優先順位より低いかまたは等しい。
例えば「+」の型を「xfy」に宣言したとすると「1+2+3」は「1+ (2+3)」と解釈されます。
逆に、「+」の型が「yfx」と宣言したとすると「1+2+3」は「(1+2)+3」と解釈されます。
もし、「+」の型が「xfx」と宣言すると、「+」の右にも左にも「+」と同じ結合優先順位を持つオペレータは置けません。したがって、「1+2+3」を1つの複合項として解釈することはできません。
また、引数が一つの複合項をオペレータ宣言する場合は、前置記法か後置記法かを決めなければなりません。
前置記法のオペレータは「fx」または「fy」という型があり、後置記法のオペレータは「xf」または「yf」という型があります。
(B)オペレータの宣言
オペレータの宣言は、標準組込述語の「op/3」を用いて行われます。
例えば、次のコマンドを入力すると「は」 というオペレータが宣言され、その大きさは「500」で、その型は「xfx」になります。
:-op(500,xfx,は).
つまり、「op」という述語の第1アーギュメントはオペレータの結合優先順位の大きさ、第2アーギュメントは型、そして、第3アーギュメントはオペレータの名前になります。
例えば、次の様にプログラムの最初にコマンドとして書いておけばいいでしょう。
:-op(500,xfx,は). :-op(600,xf,を理解する).
(C)システムが準備しているオペレータ
Prologを起動した時に、既に定義されているオペレータがいくつかあります。
Prolog起動前に、次のようなオペレータ宣言がなされていると考えてください。
:-op(1200,xfx,:-). :-op(1200,xfx,-->). :-op(1200,fx,?-). :-op(1200,fx,:-). :-op(1150,fy,module). :-op(1150,fy,help). :-op(1150,fx,public). :-op(1150,fx,mode). :-op(1150,fx,index). :-op(1150,fx,extern). :-op(1150,fx,dynamic). :-op(1150,fx,bltin). :-op(1150,fx,###). :-op(1100,xfy,;). :-op(1050,xfy,->). :-op(1000,xfy,','). :-op(900,fy,spy). :-op(900,fy,nospy). :-op(900,fy,¥+). :-op(700,xfx,is). :-op(700,xfx,¥==). :-op(700,xfx,¥=). :-op(700,xfx,@>=). :-op(700,xfx,@>). :-op(700,xfx,@=<). :-op(700,xfx,@<). :-op(700,xfx,>=). :-op(700,xfx,>). :-op(700,xfx,=¥=). :-op(700,xfx,==). :-op(700,xfx,=<). :-op(700,xfx,=:=). :-op(700,xfx,=/=). :-op(700,xfx,=..). :-op(700,xfx,=). :-op(700,xfx,<). :-op(700,xfx,:=). :-op(700,xfx,'/=='). :-op(700,xfx,#¥=). :-op(700,xfx,#>=). :-op(700,xfx,#>). :-op(700,xfx,#=<). :-op(700,xfx,#=). :-op(700,xfx,#<). :-op(580,xfy,::). :-op(580,xfx,notin). :-op(580,xfx,in). :-op(560,yfx,..). :-op(550,xfy,:). :-op(540,xfy,#). :-op(500,yfx,or). :-op(500,yfx,and). :-op(500,yfx,¥/). :-op(500,yfx,'/¥'). :-op(500,yfx,-). :-op(500,yfx,+). :-op(400,yfx,rem). :-op(400,yfx,mod). :-op(400,yfx,>>). :-op(400,yfx,<<). :-op(400,yfx,'//'). :-op(400,yfx,/). :-op(400,yfx,*). :-op(200,xfy,^). :-op(200,xfx,'**'). :-op(200,fy,¥). :-op(200,fy,-). :-op(200,fy,+).
(D)オペレータ使用上の注意
(1) まず、次の2つの項を見比べてください。
(a)f(x,y)
(b)f (x,y)
明らかに(a)は「f」というファンクタと2つのアーギュメント「x」「y」を持つ複合項です。では(b)はどうでしょうか?
これは、「f」という前置記法のオペレータが1つのアーギュメント「(x,y)」を持つものとみなされます。したがって「複合項」で述べたような通常の記法で複合項を書き表す時には、ファンクタと左カッコの間に区切り記号(空白等)を入れてはいけません。
逆に、前置記法のオペレータのアーギュメントがカッコで囲まれている時には、オペレータとアーギュメントの間に区切り記号を入れる必要があります。
(2)
複合項で述べたような通常の記法で、複合項を書き表す時に結合優先順位の大きさが1000以上のオペレータを持つ項をアーギュメントとして使う場合は、これをカッコで括ってください。
例えば、次の(c)は「assert」のアーギュメントの中に、結合優先順位の高さ1200のオペレータ「:-」 が出現しますから誤りです。(d)のように書き直してください。
(c)assert(理解する(X,風流):-理解する(X,ワビ)).
(d)assert((理解する(X,風流):-理解する(X,ワビ))).
(3)
名前と記法が同じオペレータを2つ以上定義することはできません。
しかし、名前が同じでも記法が異なれば別のオペレータしとて定義することができます。また、一度定義されたオペレータは、名前と記法が同じ述語を「op」によって宣言すると再定義されます。
(4)
前置記法のオペレータと同じ名前のアトムを使うと、そのアトムがオペレータと同じ結合優先順位を持ってしまいます。必要に応じて、このアトムをカッコで括ってください。
(5)
オペレータとしての定義を解除したいときには、結合優先順位が0のオペレータとして再定義します。
4-4.Prologの構文
4-4-1.トークン
プログラム言語の構文をBNF記法で表す場合、対応する構文木(ツリー構造)の末端(枝の先)に位置する記号はトークン(終端記号)と呼ばれます(BNF記法は「4-4-2.構文」参照)。Prolog言語の構文に現れるトークンには次のものがあります。
| 1.アトム |
|
|---|---|
| 1.1 | 「'」(シングルクォート)以外の任意の文字と「''」(シングルクォート2つ) のみからなる文字列を「'」(シングルクォート)で囲んだもの。 |
| 1.2 | 英小文字または仮名漢字で始まる文字列で、英数字、仮名漢字及びアンダーラインのみからなるもの。 |
| 1.3 | + - * / ¥ ^ < > = `(バッククォート) : . ? @ # $ & のみからなる文字列で最初の2文字が/*でないもの。 |
| 1.4 | ; ! [] {} のうちのどれか。 |
| 2.数字 | |
| 2.1 | 0から9までの数字の列 |
| 2.2 | 最初1文字が0から9のうちのどれか、2番目が引用符号で、3番目以降に0から9までの数字の列が続くもの。ただし、最初の1文字が0のときには、a~f、A~F が混じってもよい。 |
| 3.変数 | |
| 3.1 | アンダーラインで始まり、英数字、仮名漢字及びアンダーラインのみよりなる文字列。 |
| 3.2 | 英大文字で始まり、英数字、仮名漢字及びアンダーラインのみよりなる文字列。 |
| 4.ストリング | |
| 「”」以外の任意の文字と「””」のみからなる文字(長さ0でもよい。)を「””」で囲んだもの。 | |
| 5.句点文字 | |
| ( )[ ]{ }, の各文字。 |
|
| 6.コメント | |
| 6.1 | 「/*」と「*/」に囲まれた文字列で、「*/」を含まないもの。 |
| 6.2 | 「%」で始まり行末で終わる任意の文字列。 |
| 7.終止符 | |
| 長さ2の文字列で、1文字目がピリオド、2文字目の文字コードが32以下のもの。 | |
4-4-2.構文
以下に、トークンからPrologのプログラムを構成するための規則をBNF記法を用いて示します。
★BNF記法とは・・・
例えば、
<文>::=<節>|<コマンド>|<質問>
は「<文>とは、<節>か<コマンド>かあるいは<質問>である」という意味です。
つまり、「::=」の左辺が何であるのかを右辺が説明しているのです。
そして、右辺の「|」は「または」という意味を持ちます。
考えようによっては、「::=」はPrologの「:-」に対応し、「|」は「;」に対応するとみることもできます。
<文>や<節>のように「<」と「>」で囲まれた文字列は、それがどのようなものか説明されなければいけないものです。
従って、「<節>」は、単なる長さ3の文字列ではなく、どこかで定義される何かを表します。
一方次のように
<コマンド>::=:-<ゴール列><終止符>
の中に出てくる「:-」のように「<」と「>」で囲まれていない文字列は、単にその文字列を表します。
先程定義した各トークンは<アトム>、<数字>、<変数>、<ストリング>、<終止符>という形でBNF記法の中に出現します。
コメントはインタプリタに無視されますので、これは省略しました。
また、句点文字は<句点文字>という形でなく、個々の文字( ) [ ] { } , ・・の形で出現します。
結局Prologのプログラムとは、ここで定義される<文>の列です。
★Prologプログラム構成
<文>::=<節>|<コマンド>|<質問>
<コマンド>::=:-<ゴール列><終止符>
<質問>::=?-<ゴール列><終止符>
<節>::=<単位節>|<非単位節>
<単位節>::=<頭部><終止符>
<非単位節>::=<頭部>:-<ゴール列><終止符>
<頭部>::=<項>
{ただしこの<項>は<整数>,<実数>,<変数>ではない}
<ゴール列>::=<ゴール>
|<ゴール>, <ゴール列>
|<ゴール>; <ゴール列>
<ゴール>::=<項>
{ただし、この<項>は<整数>,<実数>ではない}
<項>::=<部分項(1200)>
<部分項(N)>::=<項(M)> {ただしM≦N}
<項(N)>::=<オペレータ(N,fx)>
|<オペレータ(N,fy)>
|<オペレータ(N,fx)> <部分項(N-1)> (注1)
|<オペレータ(N,fy)> <部分項(N)> (注1)
|<部分項(N-1)><オペレータ(N,xfx)><部分項(N-1)>
|<部分項(N-1 )><オペレータ(N,xfy)><部分項(N)>
|<部分項(N)><オペレータ(N,yfx )><部分項(N-1 )>
|<部分項(N-1 )><オペレータ(N,xf)>
|<部分項(N)><オペレータ(N,yf)>
<項(1000)>::=<部分項(999)>,<部分項(1000)>
<項(0)>::=<ファンクタ>(<アーギュメント列>) (注2)
|(<部分項(1200)>)
|{<部分項(1200)>}
|<リスト>
|<ストリング>
|<定数>
|<変数>
<オペレータ(N,T)>::=<ファンクタ>
{ただし、この<ファンクタ>は型T,結合の強さNで宣言されたもの}
<アーギュメント列>::=<部分項(999)>,<アーギュメント列>
|<部分項(999)>
(注1) ただし<部分項(N-1)>や<部分項(N)>がカッコでくくられている時には、<オペレータ(N,fx)>や<オペレータ(N,fy)>との間に区切り記号が必要。
(注2) <ファンクタ>と左カッコ '('の間には空白等の記号を入れてはいけません。
<リスト>::=[ ]|[<リストアーギュメント>]
<リストアーギュメント>::=<部分項(999)>, <リストアーギュメント>
|<部分項(999)>・・<部分項(999)>
|<部分項(999)>
<定数>::=<アトム>|<整数>|<実数>
<整数>::=<数字>|-<数字>
<実数>::=<数字>.<数字>
|-<数字>.<数字>
|<数字>.<数字>e<整数>
|-<数字>.<数字>e<整数>
<ファンクタ>::=<アトム>